Using the Pythagorean Theorem

I once witnessed a discussion (read: argument) between two coaches on how difficult and how far two different routes routes were to complete. I can't even remember which they were discussing, I want to say a skinny post and an out or something.

Regardless, no less of an authority on the passing game than Hal Mumme interjected between the two coaches to inform them (in typical Hal Mumme "I'm a smart guy" fashion) that there was no reason to argue, as you can easily determine how far the pass is, and that this problem was figured out thousands of years ago: Pythagoras' theorem.

To recap for those of you who do not teach high school geometry:

In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry between the three sides of a right angled triangle. A paraphrase of Pythagoras is :

In the diagram, the sum of the areas of the blue and red squares is equal to the area of the purple square.



Or, the common mnemonic about the sides of the right triangle :

a² + b² = c²

This works for any right triangle laid out on a flat plane.

To use a football example, imagine there is a QB who takes a 5 step drop (7 yards back), throwing to a receiver who runs a speed out (12 yards upfield). Let's just say that the receiver lines up 12 yards from the QB and the out part of his route takes him another 4 yards away from him (he's lined up tight I know).



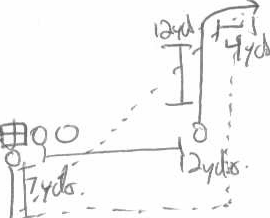
Therefore a = 7+12 = 19 and b = 12 + 4 = 16 so c^2 = 361+256 = 617. The Square root of 617 is 24.89 or roughly 25 yards.

Thus, in this example, to throw a 12 yard out cut off a 5 step drop, then QB must have the arm strength to throw a 25 yard pass on a line. This knowledge is extremely useful when evaluating quarterbacks, the importance of arm strength, what you are asking them to do with one route versus another, and, maybe most important how you want the pass thrown.